Sampling-Based Verification for Markov Models
Designing provably correct controllers for dynamical control systems under uncertainty.
Markov models are widely used to model complex probabilistic systems in reliability engineering, network processes, systems biology, and autonomous systems. However, traditional analysis methods from formal verification require that the parameters of these Markov models are precisely known. This assumption is often unrealistic in practice.
Instead, certain parameters in the transition probabilities, initial conditions, and reward function of Markov models are not exactly known. In this line of research, we consider Markov models with a prior probability distribution over the parameters. This distribution encodes prior knowledge about the possible values for the parameters. We have developed principled methods to that allow for probably approximately correct (PAC) verification of these Markov models. Our methods are based on a technique called scenario optimization and can be applied to Markov decision processes (STTT, 2022) as well as continuous-time Markov chains (CAV, 2023) with uncertain parameters.
Robust Analysis of Fault Trees
One practical application of our methods is for fault trees with uncertain fialure rates. Fault trees are widely used to predict how component faults lead to system failure in safety and economically critical assets. However, how can and should these predictions be made if there is uncertainty about the failure rates of the components? With our methods, we can analyze fault trees while being robust against uncertainty in the failure rates of components.
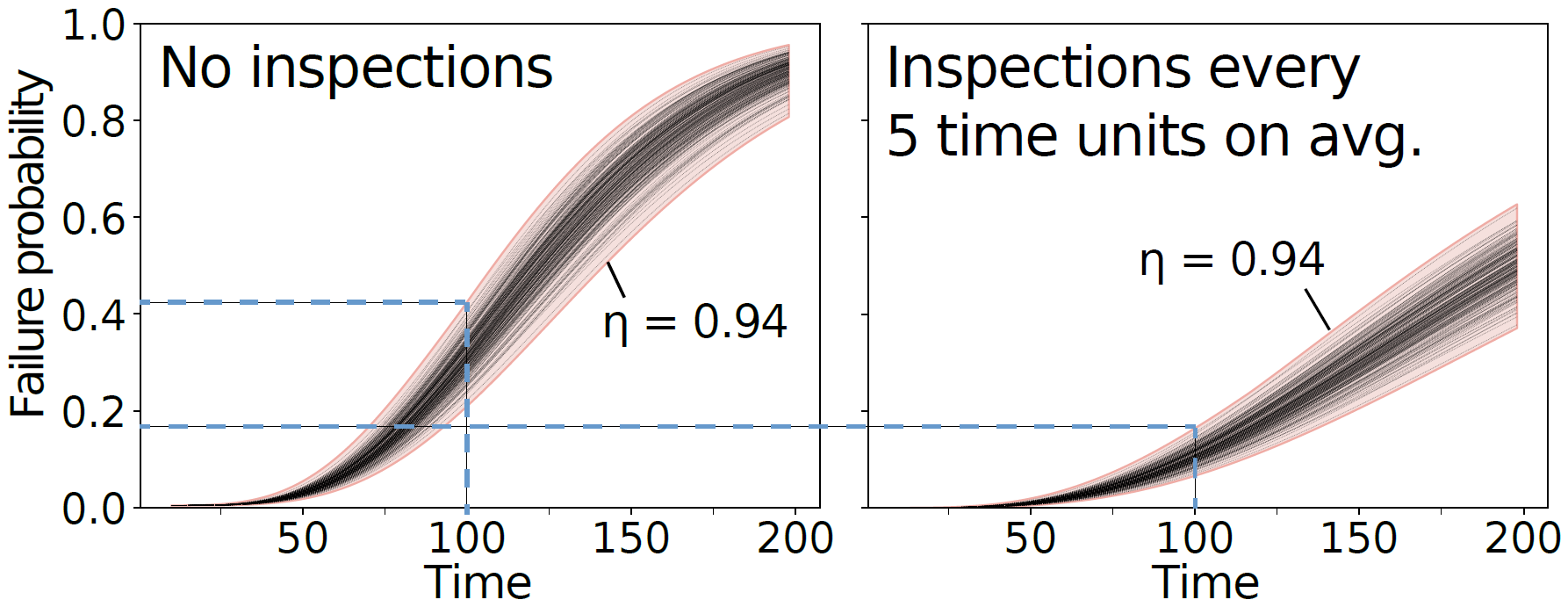
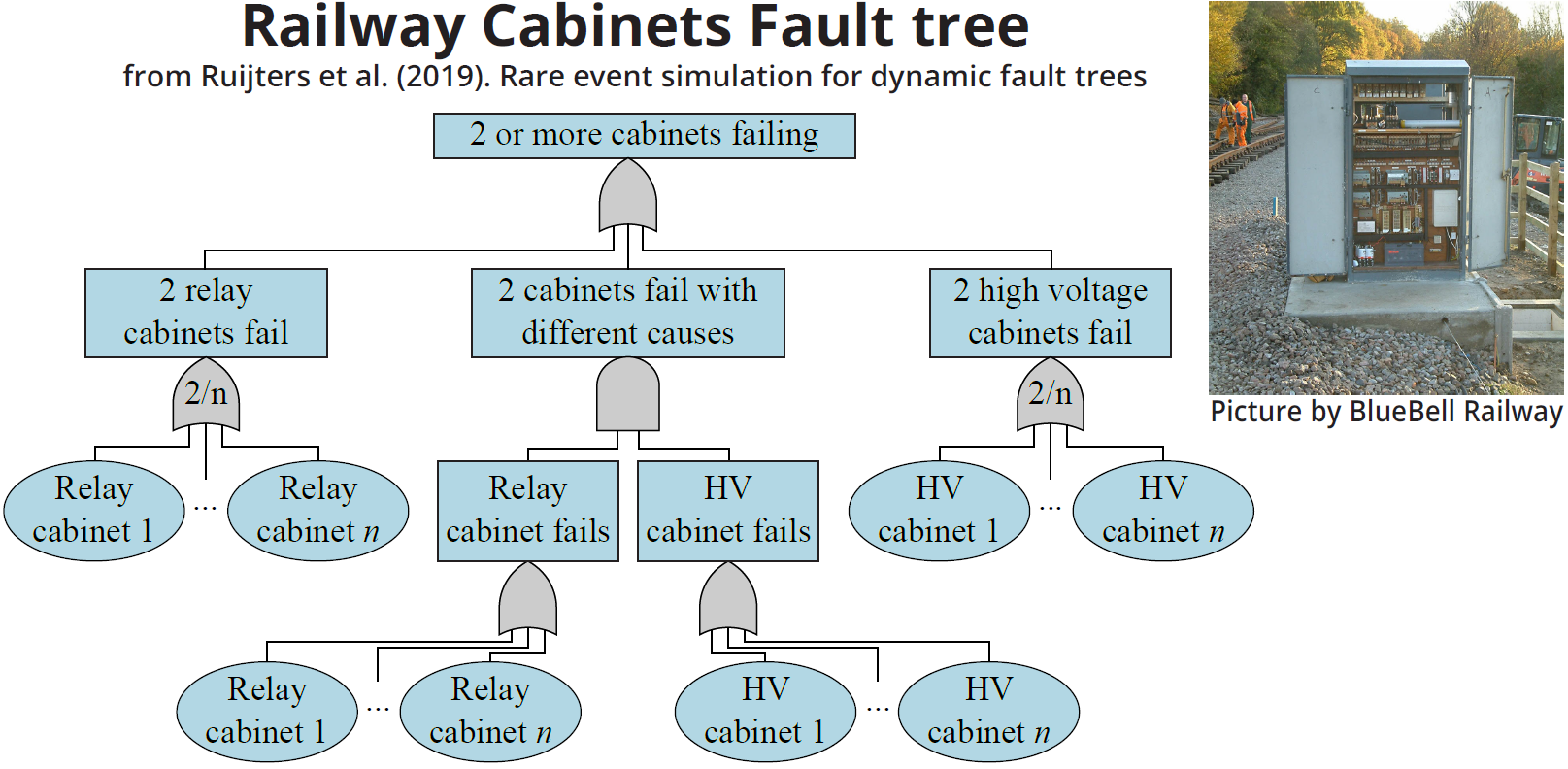
As a concrete example, consider the fault tree shown below, which models high-voltage and relay cabinets along a railway. However, two railway cabinets produced in the same factory may show different failure rates. To capture this uncertainty, we assume that the failure rates are stochastic and are sampled from a probability distribution. With our methods, we can answer the question: What can we expect for the failure probability over time of the railway cabinet?
With our methods, we can analyze the fault tree while being robust against the uncertainty in the failure rates. Concretely, we find prediction regions as in the figures below, which contain the failure probabilities over time with at least a specific (high) probability. Based on these regions, we can determine time-based maintenance policies that are robust against deviations in the failure rates.